A frequent problem in User Acquisition is to estimate ARPU (aka LTV when t->+inf) of the cohort — and a solid retention model is the foundation of any decent ARPU forecast.
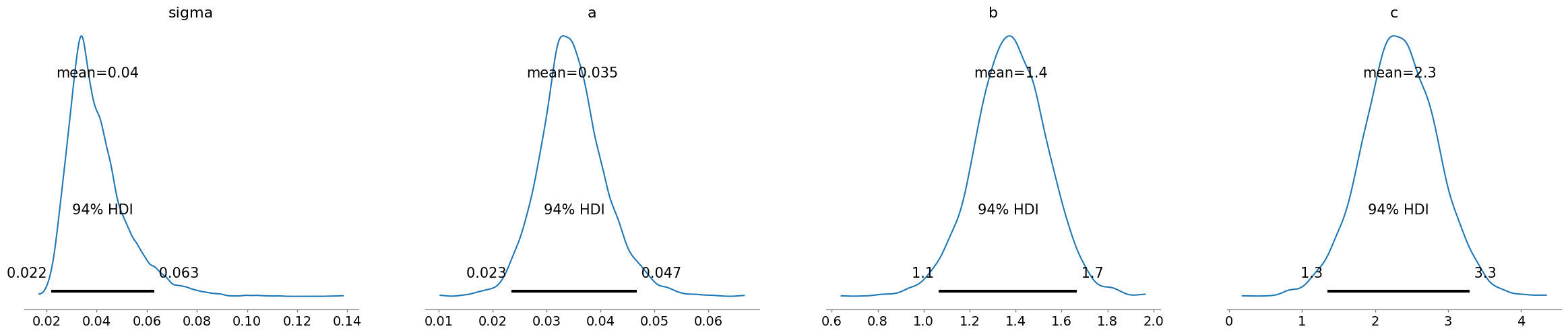
A common approach to model retention is nonlinear asymptotic regression: y(t) = a + b/(c + t)
Think of it as: most users bail early, then things flatten out. Here, (a) is your long-term survivors (the loyal 2–3%), (b) is the big early drop, and (c) controls how fast the bleeding stops.
and there is how to implement a fully bayesian version of this model to properly deal with model uncertainty. As a bonus, it's possible to extend heteroskedasticity with cohort size.
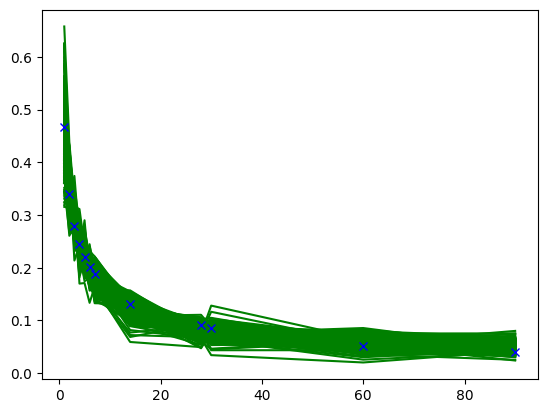
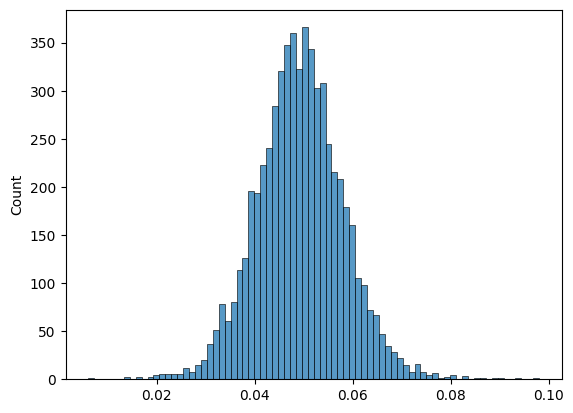
""" uv tool run \ --with pymc \ --with arviz \ --with numpy \ --with matplotlib \ --with seaborn \ --with jupyter \ jupyter notebook --port=8888 """ import pymc as pm import arviz as az import numpy as np import matplotlib.pyplot as plt import seaborn as sns # time x = np.array([1, 2, 3, 4, 5, 6, 7, 14, 28, 30, 60, 90 ]) # cohort retention y = np.array([0.468, 0.339, 0.28, 0.245, 0.22, 0.202, 0.188, 0.131, 0.0908, 0.0847, 0.052, 0.0391]) with pm.Model() as model: sigma = pm.HalfNormal('sigma', 0.1) a = pm.HalfNormal('a', 0.1) b = pm.HalfNormal('b', 5) c = pm.HalfNormal('c', 1) # add heteroskedasticity as error in tail should be smaller than in head # just make sure it doesn't explode at t=0 # ln(0+1) + 1 = 1 # ln(100 + 1) + 1 = 5.61 y_sigma = sigma / (np.log(x + 1) + 1) mu = a + b/(x + c) y = pm.Normal('y', mu=mu, sigma= y_sigma, observed=y) idata = pm.sample(1000, target_accept=0.95) ppc = pm.sample_posterior_predictive(idata, model=model) az.plot_posterior(idata) X = ppc.posterior_predictive.y.stack(z=('chain', 'draw')).to_numpy() # (T, draw) def plot(): for i in range(0,500): plt.plot(x, X[:, i], color='g') plt.plot(x, y,'x', color='b') plt.show() plot() # uncertainty on 90th day prediction sns.histplot(X[-1, :])