What is the probability that a random chord of a given circle is longer than the side of an inscribed equilateral triangle? The previous post on this subject, "Magic Chords", made two attempts to solve this problem that ended in confusion. Those attempts were based on analyzing sets of chords. I now believe that approach is too complicated and unreliable. So I begin again.

The question can be more clearly formulated as: "How likely is a randomly chosen chord of a circle longer than the side of an inscribed equilateral triangle?" The phrase "randomly chosen chord" means that each of its endpoints is equally distributed on the circle, except that the endpoints cannot coincide.

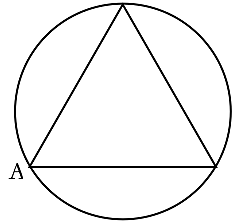
To answer this, inscribe an equilateral triangle in the circle with one vertex at an endpoint of the chord – label that endpoint A. The other end of the chord lies at a point different from A, with each such point equally likely. The vertices of the triangle divide the circle into 3 equal arcs. If the other end of the chord lies in the arc opposite A, then it is longer than a side; otherwise, it is shorter. Therefore, the chord will be longer than a side in one-third of cases and the requested probability is ⅓.

This is essentially Method 1 of the previous post, examined from a different viewpoint. What about Method 2, using parallel chords? Can it be rescued?

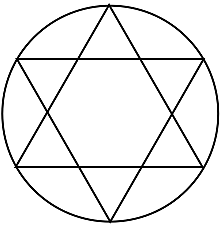
To give it a try, inscribe two different equilateral triangles in the circle, each with a side parallel to the chord. If the chord lies between the parallel sides, then it is longer than a side; otherwise, it is shorter. The six vertices of the two triangles divide the circle into 6 equal arcs. Thus, the two arcs cut off by the parallel sides constitute one-third of the circle. If the chord lies between the parallel sides, its endpoints lie on the two cut-off arcs. Therefore, the chord will be longer than a side in one‑third of cases and the requested probability is ⅓.

These analyses give credible answers to the problem. They both make a direct comparison of the length of the chord to the length of a triangle side. I view the first one, fixing an endpoint, as more reliable because it is simpler. Both analyses gain credibility by agreeing on the probability.

But why did Method 2 of the previous post give the wrong answer? Its essential difference from the parallel chords analysis above is transforming the chord to a point on a diameter to identify whether it is longer than a side. The set of points on a diameter between the parallel triangle sides is half the length of the diameter, but the corresponding chords, as identified by their endpoints, consist of one-third of the chords parallel to the given chord. Because both the points on a diameter and the chords between the parallel sides are infinite sets, there is no contradiction between the two assertions. For example, there are the same number of points on a line segment 1 unit long as on one 2 units long, but nevertheless the first is half the length of the second.

I think this cleans up the confusion arising from the previous attempts on the problem. Further, it demonstrates the power of a simple approach to problem solving.

     George Angwin, 22 January 2022
     Crescat scientia, vita excolatur.